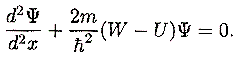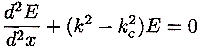| Superluminal signal velocity | ||||||||||||
| Ann. Phys. (Leipzig) 7 (1998) 7 - 8, 618 - 624 G. Nimtz Universitaet zu Koeln, II.Physikalisches Institut, Zuelpicher Str.77, D-50937 Koeln, Germany Received 20 September 1998, accepted 20 October by P. Mittelstaedt Abstract. It recently has been demonstrated that signals conveyed by evanescent modes can travel faster than light. In this report some special features of signals are introduced and investigated, for instance the fundamental property that signals are frequency band limited. Evanescent modes are characterized by extraordinary properties: Their energy is negative, they are not directly measurable, and the evanescent region is not causal since the modes traverse this region instantaneously. The study demonstrates the necessity of quantum mechanics in order to understand the superluminal signal velocity of classical evanescent modes.
|
||||||||||||
| 1 Introduction | ||||||||||||
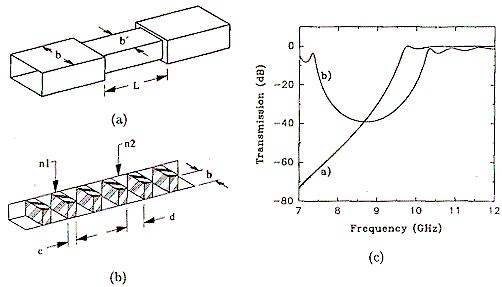
Tunneling represents the wave mechanical analogy to the propagation of evanescent modes [1]. Evanescent modes are observed, e.g. in the case of total reflection, in undersized waveguides, and in periodic dielectric heterostructures [2]. Compared with the wave solutions an evanescent mode is characterized by a purely imaginary wave number, so that the wave equation yields for the electric field E(x)
where w is the angular frequency, t the time, x the distance, k the wave number, and Kappa = ik the imaginary wave number of the evanescent mode. are shown in Fig. 1 [2]. Thus evanescent modes are characterized by an exponential attenuation and a lack of phase shift. The latter means that the mode has not spent time in the evanescent region, which in turn results in an infinite velocity in the phase time approximation neglecting the phase shift at the boundary [3]. Two examples of electromagnetic structures are shown in Fig. 1 [2] in which evanescent modes exist. The dispersion relations of the respective transmission coefficients are displayed in the same figure.
|
||||||||||||
| 2 Signals | ||||||||||||
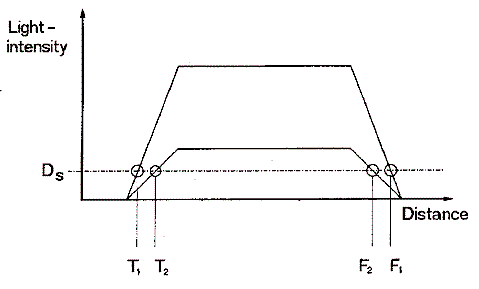
Quite often a signal is said to be defined by switching on or
off light. It is assumed that the front of the light beam informs my neighbor of my
arrival home with the speed of light. Such a signal is sketched in Fig. 2. The inevitable
inertia of the light source causes an inclination of the signal's front and tail. Due to
the detector's
sensitivity level Ds, the information about
my arrival (switching on) and departure (switching off) becomes dependent on intensity. In
this example the departure time is detected earlier with the attenuated weak signal.
magnitude as the halfwidth does not depend on
the signal's magnitude.
|
||||||||||||
| 3 An experimental result | ||||||||||||
Superluminal signal velocities have been measured by
Enders and Nimtz [4, 5, 6]. The experiments were carried out with AM microwaves in
undersized waveguides and in periodic dielectric heterostructures. The measured
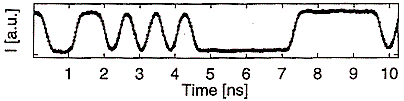
propagation time of a pulse is shown in Fig. 4. The microwave pulse has traveled either
through air or it has crossed an evanescent barrier [6]. The linewidth of the pulse
represents the signal. The experimental result is that the tunneled signal has passed the
airborne signal at a superluminal velocity of 4.7c. The measurements of the traversal time
are carried out under vacuum-like conditions at the exit of the evanescent region.
|
||||||||||||
| 4 Some implications of superluminal signal velocity | ||||||||||||
| Measured microwave signals are shown in Fig. 4. The
halfwidth (information) of the tunneled signal has traversed the evanescent region at a
velocity of 4.7c. As explained above, signals have a limited frequency spectrum since
their energy content W is always finite and detectable frequency components with In this experiment all frequency components of the signal are evanescent and move at a velocity faster than c. The beginning of the evanescent signal overtakes that of the airborne signal as seen in Fig. 4. The superluminal velocity of evanescent modes has some interesting features differing fundamentally from luminal or subluminal propagation of waves with real wave numbers. This will be discussed in the following subsections.
|
||||||||||||
| 4.1 Change of chronological order | ||||||||||||
The existence of a superluminal signal velocity
ensures the possibility of an interchange of chronological order which is established by
Radar coordinates. Let us assume an inertial system Sigma 2 moves away from system Sigma 1
with a velocity vr. Special Relativity (SR) gives the following relationship for the
travelling time Delta t and for the distance Delta x of a signal in the system Delta I
which is watched in Delta II
vr larger or equal c^2/vS is
the condition for the change of chronological order, i.e.
|
||||||||||||
| 4.2 Negative electromagnetic energy | ||||||||||||
| The Schroedinger equation yields a negative kinetic energy in
the tunneling case, since the potential U is larger than the particle's total energy W:
The same happens to evanescent modes. Within the mathematical analogy, their kinetic electromagnetic energy is negative too. The Helmholtz equation for the electric field E in a waveguide is given by the relationship
where kc is the cut-off wave
number of the evanescent regime. The quantity (k^2 - k^2/c) plays a role analogous to the
energy eigenvalue and is negative in the case of evanescent modes.
lambda 0 is the free space
wavelength of the electromagnetic wave.
where epsilon o is the
electric permeability of the vacuum.
where Z 0 is the free space impedance. In the evanescent regime k < kc the impedance is imaginary.
|
||||||||||||
| 4.3 The not-causal evanescent region | ||||||||||||
| Evanescent modes do not experience a phase shift
inside the evanescent region [2, 3]. They cross this region without consuming time. The
predicted [3] and the measured [2] time delay happens at the boundary between the wave and
the evanescent mode regime. For opaque barriers (i.e. kappa chi equal or greater than 1,
where kappa is the imaginary wave number and chi the length of the evanescent barrier) the
phase shift becomes constant with approximately 2 pi which corresponds to one oscillation
time of the mode. In fact the measured barrier traversal time was roughly equal to the
reciprocal frequency in the microwave as well as in the optical experiments, i.e. either
in the 100 ps or in the 2 fs time range independent of the barrier length [2]. The latter
behavior is called Hartman effect: the tunneling time is independent of barrier length and
has indeed been measured with microwave pulses thirty years after its prediction [5].
|
||||||||||||
| 5 Summing up | ||||||||||||
| Evanescent modes show some amazing properties which we
are not familiar with. For instance, the evanescent region is not causal since evanescent
modes do not spend time there. This is an experimental result due to the fact that the
traversal time is independent of barrier length. Another strange experience in classical physics is that evanescent fields cannot be measured. This is due to their negative energy or to the impedance mismatch. Amazingly enough, this is in analogy with wave mechanical tunneling. The energy of a signal is always finite thus resulting in a limited frequency spectrum according to Planck's energy quantum A physical signal never has an ideal front, the latter needs infinite high frequency components with a correspondingly high energy. Another consequence of the frequency band limitation of signals is, if they have only evanescent mode components, the signal may travel faster than light. Front, group, signal, and energy velocities all have the same value in vacuum. Bearing in mind the narrow frequency band of signals, the former statement holds also for the velocities of evanescent modes. In first order approximation the dispersion relation of a stop band is constant and a significant pulse reshaping does not take place. This result demonstrates that signals and effects may be transmitted with superluminal velocities provided that they are carried by evanescent modes. Stimulating discussions with V. Grunow, D. Kreimer, P. Mittelstaedt, R. Pelster, and H. Toyatt are gratefully acknowledged.
|
||||||||||||
| References | ||||||||||||
| [1] A. Sommerfeld, Vorlesungen ueber Theoretische Physik,
Band IV, Optik, Dieterich'sche Verlagsbuchhandlung (1950) [2] G. Nimtz, W. Heitmann, Prog. Quantum Electronics 21 (1997) 81 [3] Th. Hartman, J. AppI. Phys. 33 (1962) 3427 [4] A. Enders, G. Nimtz, J. Phys. I (France) 2 (1992) 1693; A.Enders, G. Nimtz, J. Phys. I (France) 3 (1993) 1089 [5] A. Enders, G. Nimtz, Phys. Rev. E 48 (1994) 632 [6] G. Nimtz et al., J. Phys. I (France) 4 (1994) 565 [7] F.E. Low, P.F. Mende, Ann. Phys. (N.Y.) 210 (1991) 380; S. Gasiorowicz Quantum Physics, Second Edition, John Wiley & Sons, New York (1996) Click
here to read about Prof. Dr. Nimtz's new tunneling experiments on a double prism |
||||||||||||