∞
There are a number of mathematical models,
that descibe a Torus in a vertical splice, or cut.

In the Cassini oval, the curve has double points at the circular points at infinity.


The images in this article can be enlarged by clicking on them.

"THE TORUS-PEARLSTRING PROPOSAL"
An Amendment to H. Minkowki's Analogon of the Cosmos as a Sphere, the Torus

Sadly, no copy of this 78 page manuscript has survived, as far as I know.
This is an attempt at recalling that paper, and bring it to it's conclusion.

It had occured to me in 1986, that the model (topology) of Albert Einstein's Universe,
which he used to describe his theory of relativity, was based on the idea of his teacher,
Hermann Minkowski, and that it was incomplete.

Instead of thinking of the topology (geometry) of the Universe as a ball (or sphere),
I visualized it as a donut, or a bagel-like shape, a torus, in proper terms.

This I thought to be so important that I went to a business supply shop and leased an electrical typewriter,
the fancy kind at the time, with a daisy-wheel and 500k of memory.

The following months were spent trying to put my vision into words and diagrams.

Much of the paper dealt with geometry, by its nature.

It described shapes, such as two dimensional triangles, three dimensional pyramids,
geometry and it drew analogies to cosmological and theoretical physics.

Whilst writing the manuscript I became very sensitive to patterns.

Our TV set was of the analogue type, with an UHF aerial on the roof.
I became curious about the interference patterns, which manifested themselves when the
TV set was tuned to the white noise of empty channels.

Now, in the West of Ireland, there are not many TV transmitters that can cause interference in the unoccupied frequencies.

Many nights, when I tuned into the white noise, a man stood in front of a blackboard,
sketching symbols during the night until the early morning hours.

So, the lecture broadcasts I picked up, were did they originate?
The signal reception was always too bad to hear any audio besides static.

This was at a time when the Irish TV stations played the National Anthem at 11pm and then shut off until 6am the next day.

It must be said, I formed a theory at the time, that these were broadcasts from the future.
Today, lacking evidence to the contrary, the more likely explanation is that I picked up the BBC Open University
rebroadcasted from Irish television deflector systems.

I can't explain the rather unusual night viewing times, of topics such as "Number Theory Metric and Topological Space" or
"Godels incompleteness theorems", but it makes sense that I was watching Open University lectures, that made their way into my subconscious.

There they gestated for a few decades.
But that is yet to come.

Without feedback or comments from the University, I proceeded to forget my experiences and writings.
My paper was not conclusive, sufficiently coherent, compelling, or mathematically described.

Many illustrations and ideas from this book I found later mirrored in books from the New Age movement.
I don't know how the graphics made it into those publications.

But I shook my head, the concepts had not been developed,
no further or deeper meaning was discovered or revealed in these New Age writings,
from my point of view.

Maybe there is a common subconscious, were all these images, symbols and archetypes float around,
only rarely surfacing. And then we struggle to make sense of it all.

The Torus-Pearlstring Proposal revisited

There are two methods of slicing a torus, horizontal or vertical.

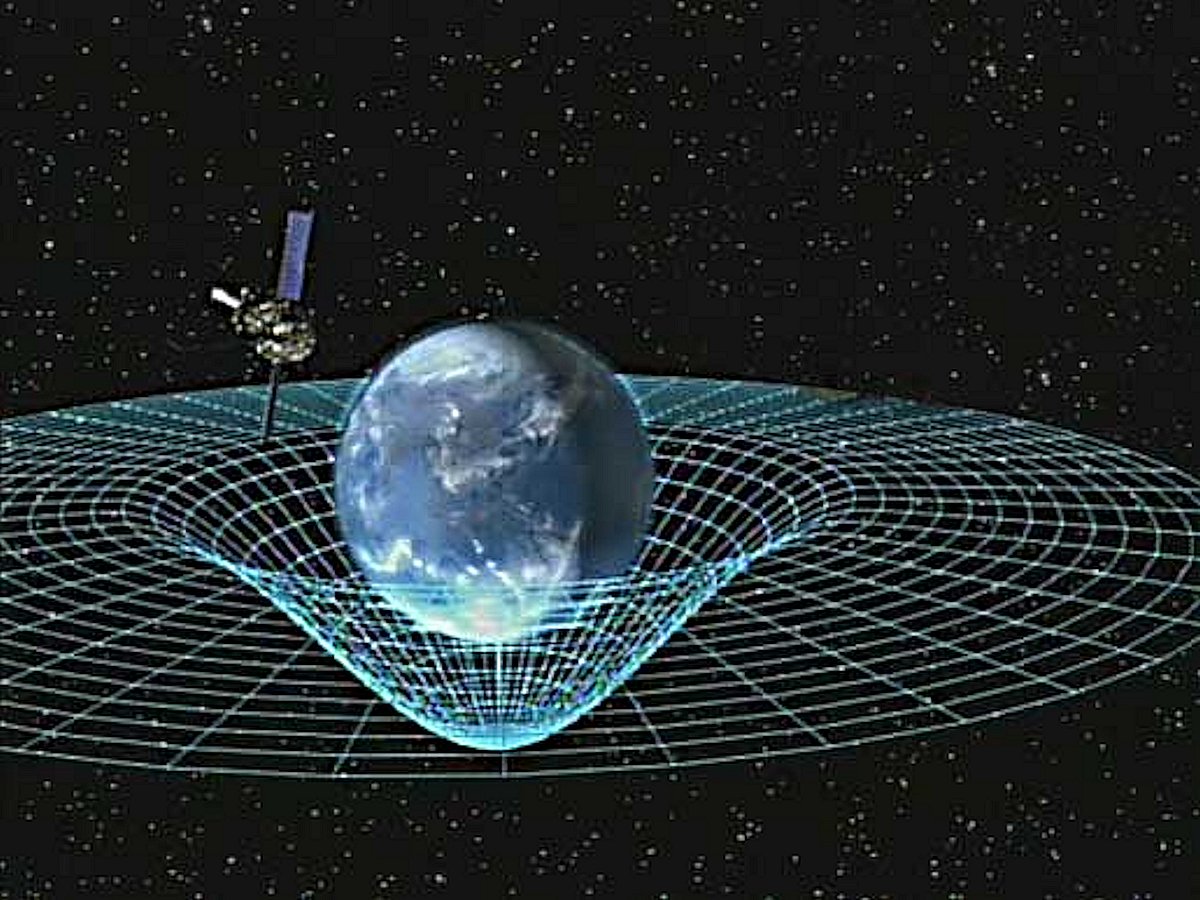1.) It can be sliced horizontally,
and the slices (depending on thickness) conform to the Minkowski space-time analogue.

This can be called the Bagel Torus.

This is what we see in space time diagrams,
describing the elasticity of a space-time sheet
under the influence of gravity.






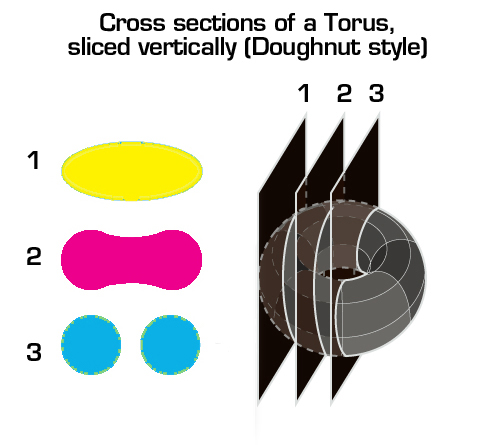2.) It can be sliced vertically, and the slices conform in the shape to the Cosmic microwave background radiation.

That slicing method results in the Doughnut Torus.

A torus sliced in half vertically in its center appears as two pearls (also described as balls or disks), see slice 3.

Depending on the slice, the shape of the disk changes.

There are a number of mathematical models,
that descibe a Torus in a vertical splice.

https://en.wikipedia.org/wiki/Cassini_oval
https://en.wikipedia.org/wiki/Spiric_section
https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli




The Torus-Pearlstring Proposal approaches the Torus as a Dupin cyclide,
which is a geometric inversion of a standard torus.
.

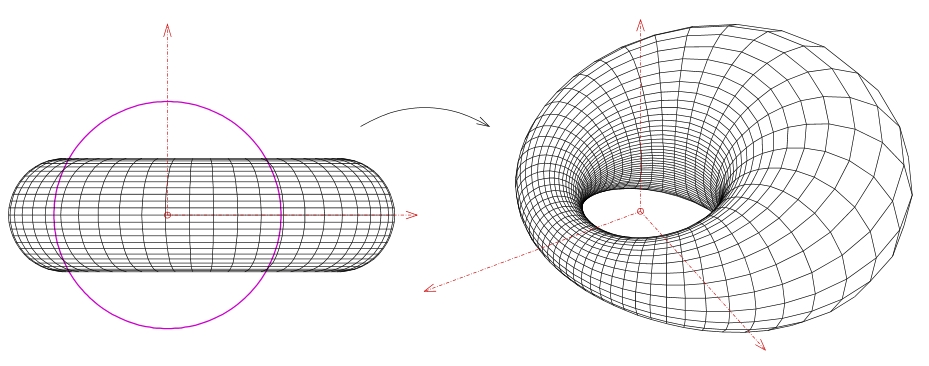
Image: Dupin Cyclide
By Ag2gaeh (Own work) [CC BY-SA 4.0 (http://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons

What I had never understood really, until today, was what the "Pearlstring" aspect of my proposal meant.
I had put it in, just because I liked the sound of it at the time...

Now, here is a possible partial answer.

Image from Brian Scott Whited: "TANGENT-BALL TECHNIQUES FOR SHAPE PROCESSING",
Georgia Institute of Technology, Doctorate of Philosophy in the College of Computing. http://hdl.handle.net/1853/31670

to be continued...
-------------------- article under this line under review -------------------

Recall
Torus Pearlstring Proposal 
The development of a fetus to a baby to an child to a teenager follows our comprehension of the World: at the beginning we have difficulty grasping at objects, because we have no grasp of three dimensions as baby. Our understanding grows as we age.

So can a toddler already navigate on the floor and soon he will start playing with balls.